STRUKTUR DATA Pertemuan 6

STRUKTUR DATA Pertemuan 6

GRAPH

Graph adalah kumpulan dati titik (node) dan garis dimana pasangan – pasangan titik (node) tersebut dihubungkan oleh segmen garis. Node ini biasa disebut simpul (vertex) dan segmen garis disebut ruas (edge)

Simpul dan ruas dalam graph dapat diperluas dengan penambahan informasi. Sebagai contoh, simpul bias diberi nomor atau label dan ruas dapat diberi nilai juga. Perluasan dengan pemberian informasi ini sangat berguna dalam penggunaan graph untuk banyak aplikasi computer. Contoh, graph dengan simpul yang merepresentasikan kota dan ruas merepresentasikan jarak yang ditempuh diantara kota – kota tersebut. (atau harga tiket pesawat antara kota – kota tersebut)

Jenis Graph

Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graph, maka graph digolongkan menjadi dua jenis :
Graph sederhana (simple graph)

• Graph yang tidak mengandung gelang maupun sisi ganda dinamakan graph sederhana

Graph tak sederhana (unsimple graph / multigraph)

• Graph yang mengandung ruas ganda atau gelang dinamakan graph tak sederhana (unsimple graph / multigraph)

Berdasarkan jumlah simpul pada suatu graph, maka secara umum graph dapat digolongkan menjadi dua jenis :

Graph berhingga (limited graph)

• Graph berhingga adalah graph yang jumlah simpulnya, n, berhingga

Graph tak berhingga (unlimited graph)

• Graph yang jumlah simpulnya, n, tidak berhingga banyaknya

Berdasarkan orientasi arah pada sisi, maka secara umum graph dibedakan atas 2 jenis :

Graph tak berarah (undirected graph)

• Graph yang sisinya tidak mempunyai orientasi arah

Graph berarah (directed graph / digraph)

DEFINISI

Graph merupakan suatu koleksi dari himpunan VG dan EG
Notasi : G = {VG, EG}
G = Graph
VG = himpunan titik (vertex graph)
EG = himpunan garis (edge graph)
Titik : node / vertex
Garis : arc / edge
Jumlah vertex dalam suatu graph disebut ORDER dari graph tresebut
Contoh : graph G dengan order = 4 (jumlah vertex = 4; a, b, c, d)
Suatu graph hanya ditentukan oleh vertex – vertex dan edge – edgenya. Posisi dari vertex – vertex dan edge – edge dalam penggambaran tidaklah penting
Graph Equivalen : penggambaran graph yang sama

Suatu graph G disebut Simple Graph, jika :

• Tidak mempunyai edge yang Self Loop (tidak ada (V,V) dalam G)
• Tidak mempunyai Multiple Edge (hanya ada (Vi, Vj) dalam G) (V1, V2, V3, … ϵ VG)

Multiple Edge adalah 1 vertex dihubungkan oleh beberapa edge

· Contoh ; pada gambar graph equivalen diatas, vertex b dihubungkan oleh edge – edge 1, 2, 3, 5, 6, 7
· Sedangkan vertex c dihubungkan oleh edge- edge 2, 3, 4
· Self Loop adalah vertex yang dihubungkan oleh edge – edge menuju edge itu sendiri
· Contoh : pada gambar graph equivalen diatas, vertex a dihubungkan oleh graph 8 menuju a kembali
· Suatu graph G disebut Connected (terhubung) jika graph G dapat dipartisi (dibagi) menjadi 2 graph dengan menghapus paling sedikit 1 edge

· Contoh yang tidak connected : suatu graph G terdiri
G = {VG, EG}
VG = {e, f, g, h}
EG = {1, 2, 3}

Path dalam graph adalah barisan dari 1 buah edge –edge yang menghubungkan 2 vertex
· Notasi :
P(Vi, Vj) = (Vi, X1)(X1, X2)(X2, Xn-1)(Xn-1, Xn)(Xn, Vj)
· Dari gambar simple graph :
P(b,d) = (b,c)(c,d)
P(b,d) = (b,c)(c,b)(b,c)(c,d)
P(b,d) = (b,d)
P(b,d) = (b,c)(c,b)(b,d)
· Length dari suatu path adalah jumlah edge – edge pada path tersebut
· Contoh : perhatikan gambar simple graph :
P(b,d) = (b,d) length = 1
= (b,c)(c,d) length = 2
= (b,c)(c,b)(b,d) length = 3
· Cycle adalah path yang memenuhi syarat sebagai berikut :

1. Tidak ada edge yang tampil lebih dari satu kali dalam barisan edge dari path tersebut
Contoh : gambar simple graph
P(b,d) = (b,c)(c,b)(b,d)
= tidak boleh

2. Path harus berbentuk P(V,V)

3. Tidak ada vertex yang dikunjungi lebih dari satu kali
Contoh : P(a,a) = (a,b)(b,c)(c,d)(d,b)(b,a)
B dikunjungi lebih dari 1x
P(b,b) = (b,c)(c,b)(b,a)(a,c)(c,b)
C & b dikunjungi 3x
Contoh Cycle : P(b,b) = (b,d)(d,c)(c,b)
· Acyclic adalah graph yang tidak mempunyai cycle
· Contoh : graph G terdiri dari
G = {VG, EG}
VG = {a,b,c,d}
EG = {1,2,3}

Catatan :
1. Graph yang simple belum tentu yang acyclic
2. Graph yang acyclic adalah graph yang simple

Graph yang berarah disebut DI-GRAPH / Directed Graph, adalah merupakan graph dimana edge – edgenya mempunyai suatu arah

Pada gambar di samping,

(a,b) = 1 arah
(b,a) = 0 arah





Graph yang tidak mempunyai arah boleh bolak – balik

Pada gambar di samping,

(a,b) = 1 arah
(b,a) = 1 arah

OUT DEGREE, IN DEGREE, DEGREE DARI SUATU VERTEX A

Vertex a mempunyai :
1. Out degree (derajat luar) = N

• Jika vertex a mempunyai N edge mengarah keluar
• Misal : vertex a memunyai 2 edge mengarah ke luar (gambar digraph diatas)

2. In degree (derajat masuk) = N

• Jika vertex a mempunyai N edge mengarah masuk ( gambar digraph diatas)

3. Degree (derajat) = N
Jika out degree a ditambah in degree a = N
Misal : vertex b
In degree = 2
Out degree = 3
Degree = 5
· Contoh : pada gambar digraph diatas;
Degree (a) = 3
Degree(b) = 5
Degree(c) = 3
Degree(d) = 5
16

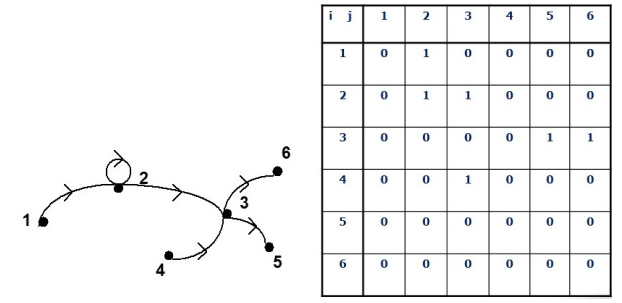
· Graph G dengan himpunan vertex V0 dan edge E0 diasumsikan graph berorder N untuk N ≥ 1
· Salah satu pendekatan untuk graph ini menggunakan matriks Adjacency dengan suatu array A ukuran N x N
A(i, j) 1 jika edge (Vi, Vj) Eij
0 jika edge (Vi, Vj) Eij

Contoh graph Undirect / matriks simetris

Contoh : graph Direct

PENGGAMBARAN NODE DIRECTORY
· Penggambaran node dalam directory dibagi dalam 2 bagian :
1. Directory
2. Himpunan link list (LL)
· Setiap record dari link list mempunyai 2 field :
4. Node indetifier
5. Suatu link yang menghubungkan elemen lain dari list (next)

Directory menggambarkan banyak node
Link list menunjukkan edge – edgenya

Kalau punya harga (untuk penggambaran manajemen proyek) penggambaran node-nya dibagi 3

Penulis : resky13211306 ~ Sebuah blog yang menyediakan berbagai macam informasi

Artikel ini dipublish oleh resky13211306 pada hari . Semoga artikel ini dapat bermanfaat.Terimakasih atas kunjungan Anda silahkan tinggalkan komentar.sudah ada 0 komentar: di postingan