STRUKTUR DATA Pertemuan 7

STRUKTUR DATA Pertemuan 7

TREE

Dalam ilmu komputer, sebuah Pohon/Tree adalah suatu struktur data yang digunakan secara luas yang menyerupai struktur pohon dengan sejumlah simpul yang terhubung.

Sebuah contoh sederhana pohon tidak terurut.

Simpul (node)
Sebuah Simpul dapat mengandung sebuah nilai atau suatu kondisi atau menggambarkan sebuah struktur data terpisah atau sebuah bagian pohon itu sendiri.Setiap simpul dalam sebuah pohon memiliki nol atau lebih simpul anak (child nodes), yang berada dibawahnya dalam pohon (menurut perjanjian, pohon berkembang ke bawah, tidak seperti yang dilakukannya di alam). Sebuah simpul yang memiliki anak dinamakan simpul ayah (parent node) atau simpul leluhur (ancestor node) atau superior. Sebuah simpul paling banyak memiliki satu ayah. Tinggi dari pohon adalah panjang maksimal jalan ke sebuah daun dari simpul tersebut. Tinggi dari akar adalah tinggi dari pohon. Kedalaman dari sebuah simpul adalah panjang jalan ke akarnya dari simpul tersebut.

Daun (leaf Nodes)

9, 14, 19, 67 dan 76 adalah daun.

Semua simpul yang berada pada tingkat terendah dari pohon dinamakan daun (leaf node). Sejak mereka terletak pada tingkat paling bawah, mereka tidak memiliki anak satupun. Seringkali, daun merupakan simpul terjauh dari akar. Dalam teori grafik, sebuah daun adalah sebuah sudut dengan tingkat 1 selain akar (kecuali jika pohonnya hanya memiliki satu sudut; maka akarnya adalah daunnya juga). Setiap pohon memiliki setidaknya satu daun.

Dalam pohon berdasarkan genetic programming sebuah daun (juga dibilang terminal) adalah bagian terluar dari sebuah program pohon. Jika dibandingkan dengan fungsinya atau simpul dalam, daun tidak memiliki argumen. Di banyak kasus dalam daun-GP input ke programnya.

Simpul dalam (Internal nodes)

Sebuah simpul dalam adalah semua simpul dari pohon yang memiliki anak dan bukan merupakan daun. Beberapa pohon hanya menyimpan data di dalam simpul dalam, meskipun ini memengaruhi dinamika penyimpanan data dalam pohon. Sebegai contoh, dengan daun yang kosong, seseorang dapat menyimpan sebuah pohon kosong dengan satu daun.
Bagaimanapun juga dengan daun yang dapat menyimpan data, tidak dimungkinkan untuk menyimpan pohon kosong kecuali jika seseorang memberikan beberapa jenis penanda data di daun yang menandakan bahwa daun tersebut seharusnya kosong (dengan demikian pohon itu seharusnya kosong juga).

Sebaliknya, beberapa pohon hanya menyimpan data dalam daun, dan menggunakan simpul dalam untuk menampung metadata yang lain, seperti jarak nilai dalam sub pohon yang berakar pada simpul tersebut. Jenis pohon ini berguna untuk jarak yang meragukan.


Sub pohon (Subtrees)
Sebuah sub pohon adalah suatu bagian dari pohon struktur data yang dapat dilihat sebagai sebuah pohon lain yang berdiri sendiri. Simpul apapun dalam pohon P, bersama dengan seluruh simpul dibawahnya, membentuk sebuah sub pohon dari P. Sub pohon yang terhubung dengan akar merupakan keseluruhan pohon tersebut. Sub pohon yang terhubung dengan simpul lain manapun dinamakan sub pohon asli (proper subtree)

Penyusunan pohon

Terdapat dua jenis pohon. Sebuah pohon tidak terurut (unordered tree) adalah sebuah pohon dalam arti struktural semata-mata, yang dapat dikatakan memberikan sebuah simpul yang tidak memiliki susunan untuk anak dari simpul tersebut. Sebuah pohon dengan suatu susunan ditentukan, sebagai contoh dengan mengisi bilangan asli berbeda ke setiap anak dari simpul tersebut, dinamakan sebuah pohon terurut (ordered tree), dan struktur data yang dibangun di dalamnya dinamakan pohon terurut struktur data(ordered tree data structures). Sejauh ini pohon terurut merupakan bentuk umum dari pohon struktur data. Pohon biner terurut merupakan suatu jenis dari pohon terurut.


Hutan (Forest)

Sebuah hutan adalah sebuah himpunan yang terdiri dari pohon terurut. Lintasan inorder,preorder, dan postorder didefinisikan secara rekursif untuk hutan.

inorder

• lewati inorder hutan yang dibentuk oleh sub pohon yang pertama dalam hutan, jika ada
• kunjungi akar dari pohon pertama.
• lewati inorder hutan yang dibentuk oleh sisa pohon dalam hutan, jika ada.

preorder

• kunjungi akar dari pohon pertama.
• lewati preorder hutan yang dibentuk oleh sub pohon yang pertama dalam hutan, jika ada
• lewati preorder hutan yang dibentuk oleh sisa pohon dalam hutan, jika ada.

postorder

• lewati postorder hutan yang dibentuk oleh sub pohon yang pertama dalam hutan, jika ada
• lewati postorder hutan yang dibentuk oleh sisa pohon dalam hutan, jika ada.
• kunjungi akar dari pohon pertama.

Penggambaran pohon

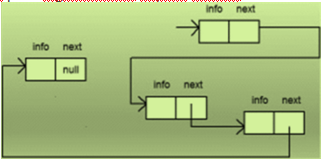
Ada banyak cara untuk menggambarkan pohon; pada umumnya penggambaran mewakili simpul sebagai rekor yang dialokasikan pada heap (bedakan dengan heap struktur data) yang mengacu pada anaknya, ayahnya, atau keduanya, atau seperti data materi dalam array, dengan hubungan diantaranya ditentukan oleh posisi mereka dalam array (contoh binary heap).


Pohon sebagai grafik

Dalam teori grafik, sebuah pohon adalah sebuah grafik asiklis yang terhubung. Pohon yang berakar merupakan sebuah grafik dengan sudut tunggal di luar sebagai akar. Dalam kasus ini, dua sudut apapun yang terhubung dengan sebuah sisi mewarisi hubungan orang tua dan anak. Sebuah grafik asiklis dengan bermacam-macam komponen yang terhubung atau himpunan dari pohon-pohon yang berakar kadang-kadang dipanggil hutan


Metode traversal

Melangkah melalui materi dari pohon, dengan arti dari hubungan antara orang tua dan anak, dinamakan menelusuri pohon, dan tindakannya adalah sebuah jalan dari pohon. Seringkali, sebuah operasi mungkin dapat dilakukan sebagai penunjuk ysng mengacu pada simpul khusus. Sebuah penelusuran dimana setiap simpul ayah dikunjungi sebelum anaknya dinamakan pre-order walk; sebuah penelusuran dimana anaknya dikunjungi sebelum ayahnya masing-masing dinamakan post-order walk.

contoh tugas tree binary

contoh tugas tree binary

Contoh soal Tree dan Jawabannya

Tree 1





Tree 2





Tree 3




1. Tentukan root masing masing tree
2. tentukan leaf masing masing tree
3. rubahlah menjadi binary tree
4. tentukan Height dan Width
5. dari ke 3 tree tersebut rubahlah menjadi binary tree
6. dari soal diatas bentuklah 3 aktifitas dalam binary tree
    Pre order
    In order
    Post order


jawaban

1. tree 1 = A, tree 2 = 1, tree 3 =A1

2.tree 1 = (W,P,R,S,Z,H,I,J,U,V,X,L,Y,N,O)
   tree 2 = (3,4,7,8,9,10)
   tree 3 = (A4,A5,A6)

3. Tree1



Tree 2



Tree 3



4. Tree 1 Height = 6
               Widht = 15

    Tree 2 Height = 5
               Width = 6

    Tree 3 Height = 4
               Width = 3



5.  


6. Tree 1 
    Pre order Transversal   = A B W G H I P Q R S T Z C J K U V X D L E M N Y F O
    In Order Transversal    = I H G P Q R S T Z A B W C J K U V X D L E M N Y F O
    Post Order Trensversal =  I Z T S R Q  P G W B X V U K N Y M L J O FE D C A

  Tree 2 
    Pre order Transversal   = 1 2 3 4 5  6 7 8 9 10
    In Order Transversal    = 7 6 8 9 10 1 4 5 3 2
    Post Order Trensversal =  7 6 8 9 10 4 5 3 2 1

 Tree 3 
    Pre order Transversal   = A1 A2 A3 A4 A5 A6
    In Order Transversal    = A6 A5 A4 A3 A1 A2
    Post Order Trensversal = A6 A5 A4 A3 A2 A1

STRUKTUR DATA Pertemuan 6

STRUKTUR DATA Pertemuan 6

GRAPH

Graph adalah kumpulan dati titik (node) dan garis dimana pasangan – pasangan titik (node) tersebut dihubungkan oleh segmen garis. Node ini biasa disebut simpul (vertex) dan segmen garis disebut ruas (edge)

Simpul dan ruas dalam graph dapat diperluas dengan penambahan informasi. Sebagai contoh, simpul bias diberi nomor atau label dan ruas dapat diberi nilai juga. Perluasan dengan pemberian informasi ini sangat berguna dalam penggunaan graph untuk banyak aplikasi computer. Contoh, graph dengan simpul yang merepresentasikan kota dan ruas merepresentasikan jarak yang ditempuh diantara kota – kota tersebut. (atau harga tiket pesawat antara kota – kota tersebut)

Jenis Graph

Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graph, maka graph digolongkan menjadi dua jenis :
Graph sederhana (simple graph)

• Graph yang tidak mengandung gelang maupun sisi ganda dinamakan graph sederhana

Graph tak sederhana (unsimple graph / multigraph)

• Graph yang mengandung ruas ganda atau gelang dinamakan graph tak sederhana (unsimple graph / multigraph)

Berdasarkan jumlah simpul pada suatu graph, maka secara umum graph dapat digolongkan menjadi dua jenis :

Graph berhingga (limited graph)

• Graph berhingga adalah graph yang jumlah simpulnya, n, berhingga

Graph tak berhingga (unlimited graph)

• Graph yang jumlah simpulnya, n, tidak berhingga banyaknya

Berdasarkan orientasi arah pada sisi, maka secara umum graph dibedakan atas 2 jenis :

Graph tak berarah (undirected graph)

• Graph yang sisinya tidak mempunyai orientasi arah

Graph berarah (directed graph / digraph)

DEFINISI

Graph merupakan suatu koleksi dari himpunan VG dan EG
Notasi : G = {VG, EG}
G = Graph
VG = himpunan titik (vertex graph)
EG = himpunan garis (edge graph)
Titik : node / vertex
Garis : arc / edge
Jumlah vertex dalam suatu graph disebut ORDER dari graph tresebut
Contoh : graph G dengan order = 4 (jumlah vertex = 4; a, b, c, d)
Suatu graph hanya ditentukan oleh vertex – vertex dan edge – edgenya. Posisi dari vertex – vertex dan edge – edge dalam penggambaran tidaklah penting
Graph Equivalen : penggambaran graph yang sama

Suatu graph G disebut Simple Graph, jika :

• Tidak mempunyai edge yang Self Loop (tidak ada (V,V) dalam G)
• Tidak mempunyai Multiple Edge (hanya ada (Vi, Vj) dalam G) (V1, V2, V3, … ϵ VG)

Multiple Edge adalah 1 vertex dihubungkan oleh beberapa edge

· Contoh ; pada gambar graph equivalen diatas, vertex b dihubungkan oleh edge – edge 1, 2, 3, 5, 6, 7
· Sedangkan vertex c dihubungkan oleh edge- edge 2, 3, 4
· Self Loop adalah vertex yang dihubungkan oleh edge – edge menuju edge itu sendiri
· Contoh : pada gambar graph equivalen diatas, vertex a dihubungkan oleh graph 8 menuju a kembali
· Suatu graph G disebut Connected (terhubung) jika graph G dapat dipartisi (dibagi) menjadi 2 graph dengan menghapus paling sedikit 1 edge

· Contoh yang tidak connected : suatu graph G terdiri
G = {VG, EG}
VG = {e, f, g, h}
EG = {1, 2, 3}

Path dalam graph adalah barisan dari 1 buah edge –edge yang menghubungkan 2 vertex
· Notasi :
P(Vi, Vj) = (Vi, X1)(X1, X2)(X2, Xn-1)(Xn-1, Xn)(Xn, Vj)
· Dari gambar simple graph :
P(b,d) = (b,c)(c,d)
P(b,d) = (b,c)(c,b)(b,c)(c,d)
P(b,d) = (b,d)
P(b,d) = (b,c)(c,b)(b,d)
· Length dari suatu path adalah jumlah edge – edge pada path tersebut
· Contoh : perhatikan gambar simple graph :
P(b,d) = (b,d) length = 1
= (b,c)(c,d) length = 2
= (b,c)(c,b)(b,d) length = 3
· Cycle adalah path yang memenuhi syarat sebagai berikut :

1. Tidak ada edge yang tampil lebih dari satu kali dalam barisan edge dari path tersebut
Contoh : gambar simple graph
P(b,d) = (b,c)(c,b)(b,d)
= tidak boleh

2. Path harus berbentuk P(V,V)

3. Tidak ada vertex yang dikunjungi lebih dari satu kali
Contoh : P(a,a) = (a,b)(b,c)(c,d)(d,b)(b,a)
B dikunjungi lebih dari 1x
P(b,b) = (b,c)(c,b)(b,a)(a,c)(c,b)
C & b dikunjungi 3x
Contoh Cycle : P(b,b) = (b,d)(d,c)(c,b)
· Acyclic adalah graph yang tidak mempunyai cycle
· Contoh : graph G terdiri dari
G = {VG, EG}
VG = {a,b,c,d}
EG = {1,2,3}

Catatan :
1. Graph yang simple belum tentu yang acyclic
2. Graph yang acyclic adalah graph yang simple

Graph yang berarah disebut DI-GRAPH / Directed Graph, adalah merupakan graph dimana edge – edgenya mempunyai suatu arah

Pada gambar di samping,

(a,b) = 1 arah
(b,a) = 0 arah





Graph yang tidak mempunyai arah boleh bolak – balik

Pada gambar di samping,

(a,b) = 1 arah
(b,a) = 1 arah

OUT DEGREE, IN DEGREE, DEGREE DARI SUATU VERTEX A

Vertex a mempunyai :
1. Out degree (derajat luar) = N

• Jika vertex a mempunyai N edge mengarah keluar
• Misal : vertex a memunyai 2 edge mengarah ke luar (gambar digraph diatas)

2. In degree (derajat masuk) = N

• Jika vertex a mempunyai N edge mengarah masuk ( gambar digraph diatas)

3. Degree (derajat) = N
Jika out degree a ditambah in degree a = N
Misal : vertex b
In degree = 2
Out degree = 3
Degree = 5
· Contoh : pada gambar digraph diatas;
Degree (a) = 3
Degree(b) = 5
Degree(c) = 3
Degree(d) = 5
16

· Graph G dengan himpunan vertex V0 dan edge E0 diasumsikan graph berorder N untuk N ≥ 1
· Salah satu pendekatan untuk graph ini menggunakan matriks Adjacency dengan suatu array A ukuran N x N
A(i, j) 1 jika edge (Vi, Vj) Eij
0 jika edge (Vi, Vj) Eij

Contoh graph Undirect / matriks simetris

Contoh : graph Direct

PENGGAMBARAN NODE DIRECTORY
· Penggambaran node dalam directory dibagi dalam 2 bagian :
1. Directory
2. Himpunan link list (LL)
· Setiap record dari link list mempunyai 2 field :
4. Node indetifier
5. Suatu link yang menghubungkan elemen lain dari list (next)

Directory menggambarkan banyak node
Link list menunjukkan edge – edgenya

Kalau punya harga (untuk penggambaran manajemen proyek) penggambaran node-nya dibagi 3

STRUKTUR DATA Pertemuan 5

STRUKTUR DATA Pertemuan 5

LINKED LIST

· Dalam suatu linear list kita dapat melakukan operasi penyisipan / penghapusan atas elemen-elemennya pada sembarang posisi

· Misalkan ada 1500 item yang merupakan elemen dari suatu linear list

· Jika elemen ke 56 akan kita keluarkan, maka elemen ke 1 s/d elemen ke 55 tidak akan berubah posisinya pada linear list tersebut

· Tetapi elemen ke 57 akan menjadi elemen ke 56, elemen ke 58 akan menjadi elemen ke 57 dst

· Selanjutnya, jika kita sisipkan satu elemen pada posisi setelah elemen ke 41 maka elemen ke 42 s/d elemen ke 1500 akan berubah posisinya

· Untuk menyatakan keadaan diatas diperlukan suatu konsep yang berbeda dengan konsep sekuensial sebelumnya

· Linked list merupakan suatu cara non sekuensial yang digunakan untuk merepresentasikan suatu data

ARRAY	LINKED LIST
Statis	Dinamis
Penambahan / penghapusan data terbatas	Penambahan / Pengahapusan data tidak terbatas
Random Access	Sequential Access
Penghapusan array tidak mungkin	Penghapusan linked list mungkin

DEFINISI

· Linked list (one way list) adalah suatu kumpulan elemen data (yang disebut sebagai node) dimana urutannya ditentukan oleh suatu pointer

· Setiap elemen (node) dari suatu linked list terdiri atas 2 bagian yaitu :

1. Info, berisi informasi tentang elemen data yang bersangkutan
2. Next (linked field / next pointer field), berisi alamat dari elemen (node) selanjutnya yang dituju



BENTUK NODE SINGLE LINKED LIST NON CIRCULAR


Pengertian :


· Single : artinya field pointernya hanya satu buah saja dan satu arah serta pada akhir node, pointernya menunjuk NULL


· Linked list : artinya node – node tersebut saling terhubung satu sama lain


· Setiap node pada linked list mempunyai field yang berisi pointer ke node berikutnya, dan juga memiliki field yang berisi data


· Node terakhir akan menunjuk ke null, yang akan digunakan sebagai kondisi berhenti pada saat pembacaan isi linked list


· Berikut ini sebuah contoh linked list yang terdiri atas 4 node




· Pada node ke 4 field nextnya berisi null artinya node ke 4 tersebut adalah node terakhir


· Node – node dalam linked list tidak harus selalu di gambarkan parallel seperti pada gambar diatas. Linked list pada contoh diatas dapat pula digambarkan seperti berikut








· Catatan :


· Ada 2 hal yang menjadi kerugian dengan representasi suatu data dengan linked list ini yaitu


2. Di perlukan ruang tambahan untuk menyatakan / tempat field pointer


3. Diperlukan waktu yang lebih banyak untuk mencari suatu node ke dalam linked list


· Sedangkan keuntungannya adalah


5. Jenis data yang berbeda dapat di link


6. Operasi remove / insert hanya dilakukan dengan mengubah pointernya saja


OPERASI DASAR PADA LINKED LIST


Ada beberapa aturan yang dapat didefinisikan pada operasi didalam linked list yaitu


· Jika P adalah suatu variabel pointer, maka nilainya adalah alamat / lokasi dari variabel lain yang dituju


· Operasi yang didefinisikan pada suatu variabel pointer adalah


1. Test apakah sama dengan null


2. Test untuk kesamaan dengan variabel pointer lain


3. Menetapkan sama dengan null


4. Menetapkan menuju ke node lain


· Notasi yang didefinisikan sehubungan dengan operasi diatas adalah


1. Node (P) artinya node yang ditunjuk oleh pointer P


2. INFO (P) artinya nilai info dari node yang ditunjuk pointer P


3. NEXT (P) artinya hubungan (link) selanjutnya dari node yang ditunjuk oleh pointer P


· Sebagai contoh, perhatikan linked list dibawah ini







NODE (P) : node yang ditunjuk oleh P yaitu node pertama


· INFO (P) : A


· NEXT (P) : node ke 2


· INFO(NEXT(NEXT(P))) = C


· MENGHAPUS SUATU NODE DARI LINKED LIST (REMOVE)


· Untuk menghapus node dalam linked list digunakan procedure FREENODE


· Jika Q adalah suatu variabel pointer, maka FREENODE (Q) akan menyebabkan node yang ditunjuk oleh variabel pointer Q dihapus dari linked list


· Perhatikan linked list berikut


Langkah 1

Q := NEXT(P)

Langkah 2

NEXT(P) := NEXT (Q)

· Langkah 3

FREENODE(Q)
· Procedure freenode (Q)

2. NEXT (Q) := avail

3. · INFO (Q) := NULL
· Avail := Q

MENYISIPKAN SUATU NODE KEDALAM LINKED LIST·
Untuk menyisipkan node kedalam linked list digunakan procedure GETNODE
· Jika NEW adalah suatu variabel pointer, maka GETNODE(NEW) akan menyebabkan node yang ditunjuk oleh variabel pointer NEW di sisipkan ke dalam linked list

PROCEDURE GETNODE (NEW)

If Avail = Null
Then out-of-free-space
· Else begin
Getnode := avail;

· Avail := Next(Avail);

· Next(Getnode) := Null;
· End;

ALGORITMA MENYISIPKAN SEBUAH NODE
· Getnode(NEW);
· Info(NEW) := Name;

· Q := Next(P)
· Next(P) := NEW



· Next(NEW) := Q

LOGIKA LINKED LIST PADA ARRAY
Jika tidak menggunakan logika linked list (pada umumnya dalam meng-input data digunakan cara sequential)

Jika menggunakan logika linked list

MENDEFINISIKAN LINKED LIST DALAM PASCAL

Type nodeptr = ^nodetype;
Nametype = packed array[1..10] of char;
Nodetype = record
Info : nametype;
Next : nodeptr;
End;
Var p : nodeptr;
Nodeptr : nodetype;
Catatan :
· P ^. Info : info dari node yang ditunjuk oleh pointer P
· P ^. Next : next dari node yang ditunjuk oleh pointer P
· P := nil : pointer P berisi nilai Null
· New (P) : fungsi getnode dalam pascal
· Dispose(P) : procedure freenode dalam pascal

MENGHAPUS SEBUAH NODE DALAM PASCALProcedure removaf(p:nodeptr, var out:nametype);
Var q : nodeptr;
Begin
If (p^.next = nil)
Then UNDERFLOW-CONDITION
Else begin
q := p^.next;
p^.next := q^.next;
out := q^.info;
dispose (q);
end;
end;

MENYISIPKAN SEBUAH NODE DALAM PASCAL

Procedure inseraf(p:nodeptr, in:nametype);
Var q : nodeptr;
Begin
New(q);
q^.info := in;
q^.next := p^.next;
p^.next := q;
end;

INSERT-END

Penyisipan pada akhir dari suatu linked list (linked list antrean) dalam Pascal

Procedure inserend (first : nodeptr, in : nametype);
Var newnode, q : nodeptr;
Begin
New(newnode);
Newnode^.info := in;
Newnode^.next := nil;
q := first;
do while (q^. <> nil)
q := q^.next;
q^.next := newnode;
end;

Jika sebuah linked list digunakan untuk menggambarkan suatu antrean, dalam hal ini pointer dapat langsung menunjuk ke rear / akhir dari antrean untuk menghindari pengulangan melalui semua node untuk menemukan terakhir

Procedure inserend (in : nametype, var rear : nodeptr);
Var newnode : nodeptr;
Begin
New(newnode);
newnode^.info := in;
newnode^.next := nil;
rear^.next :=newnode;
rear := newnode;
end;

STRUKTUR DATA Pertemuan 4

STRUKTUR DATA Pertemuan 4

Notasi Infix,Postfix dan Prefix

1.      Notasi Infix

 Contoh : x + y

a)  Operator ditulis diantara operand.

b)  Sebagai contoh A* (B + C) / D yang biasa berarti “tambahkan B dan C terlebih dahulu, dan kalikan dengan A. Setelah itu bagi dengan D.”

c)  Notasi Infix membutuhkan informasi ekstra :

·     Rule mengenai operator precedence.

·     Assosiativem dan tanda kurung ().

2.      Notasi Postfix ”Reserve Polish Notation”

Contoh : x y +

a)     Operator ditulis sebagai operand.

Contoh : ABC + * D /

b)     Operator selalu terurut dari kiri ke kanan, dan kurang tidak dapat dipergunakan untuk mengubah urutan operasi.

Contoh : pada notasi diatas, tanda + dikerjakan terlebih dahulu sebelum *.

c)     Jika bertemu operator, maka operasi aritmatik akan sesegera mungkin dikerjakan.

Contoh : jika ditemukan +, maka B dan C akan segera dijumlahkan.

a)     Setelah itu A akan dikalikan dengan hasil B + C, dan hasil keseluruhan akan dibagikan dengan D.

 3.      Notasi Prefix “Polish Notation”

contoh : x + y

a)     Operator dituliskan sebelum operand. Pada contoh sebelumnya, jika dituliskan dalam prefix adalah : / * A + B C D.

b)     Sebagaimana Postfix, operator dievaluasi dari kiri ke kanan.

c)     Operator akan mengambil dua nilai operand terdekat pada kanan operator.

d)     Meski pada prefix operator dievaluasi dari kiri ke kanan,namun prefix menggunakan nilai pada bagian kanan. Jika nilai operand melibatkan komputasi, maka akan mengubah urutan operator.

(A + B) * C / (D -F)

Postfix A | B | + | C | D | F | -

Prefix 1 | - | D | F | * | C | + | A | B

Contoh :

Infix	Postfix	Prefix	Notes
A * B + C / D	A B * C D / +	+ * A B / C D	Dikalikan A dan B bagi dengan C dengan D, tambahkan hasilnya.
A * (B + C) /D	A B C + * D /	/ * A + B C D	Tambahkan B dan C kalikan dengan A bagi dengan D.
A * (B + C /D)	A B C D / + *	* A + B / C D	Bagi C dengan D, tambahkan B, kalikan dengan A.

STRUKTUR DATA Pertemuan 3

STRUKTUR DATA Pertemuan 3

STACK

A. Linear list

      Linear List adalah suatu struktur data yang merupakan himpunan terurut. Misal didefinisikan  suatu linear list A yang terdiri atas T buah elemen sebagai berikut :

A = [a1, a2, .........., aT]

Jika T = 0, maka A dikatakan sebagai “Null List”.

Suatu elemen dari sembarang posisi pada linear list A dapat dihilangkan. Sebaliknya, suatu elemen baru dapat dimasukkan ke dalam list dan dapat menempati sembarang posisi pada list tersebut. Jadi suatu linear list dapat berkurang atau bertambah setiap saat.

B. Definisi stack

      Stack adalah suatu bentuk khusus dari linear list di mana operasi penyisipan dan penghapusan atas elemen-elemennya hanya dapat dilakukan pada satu sisi saja yang disebut sebagai “TOP”.

Misal diberikan Stack S sebagai berikut :

      S = [ S1, S2, .........., ST ]   maka TOP(S) = ST.

Operasi Dasar Pada Stack

      Ada empat operasi dasar yang didefinisikan pada stack, yaitu :

      1.      CREATE(stack)

      2.      ISEMPTY(stack)

      3.      PUSH(elemen,stack)

      4.      POP(stack)

CREATE

        Operator ini berfungsi untuk membuat sebuah stack kosong dan didefinisikan bahwa:  NOEL(CREATE(S)) = 0 dan TOP(CREATE(S)) = null

ISEMPTY

        Operator ini berfungsi untuk menentukan apakah suatu stack adalah stack kosong. Operasinya akan bernilai boolean, dengan definisi sebagai berikut :

            ISEMPTY(S) = true, jika S adalah stack kosong

                                   = false, jika S bukan stack kosong

      atau

            ISEMPTY(S) = true, jika NOEL(S) = 0

                                   = false, jika NOEL(S) 0

      Catatan :  ISEMPTY(CREATE(S)) = true.

PUSH

         Operator ini berfungsi untuk menambahkan satu elemen ke dalam stack. Notasi yang digunakan adalah :

            PUSH(E,S)

Artinya : menambahkan elemen E ke dalam stack S.

Elemen yang baru masuk ini akan menempati posisi TOP.

Jadi : TOP(PUSH(E,S)) = E.

Akibat dari operasi ini jumlah elemen dalam stack akan bertambah, artinya NOEL(S) menjadi lebih besar atau stack menjadi tidak kosong (ISEMPTY(PUSH(E,S)) = false).

POP

         Operator ini berfungsi untuk mengeluarkan satu elemen dari dalam stack. Notasinya :

                        POP(S)

Elemen yang keluar dari dalam stack adalah elemen yang berada pada posisi TOP. Akibat dari operasi ini jumlah elemen stack akan berkurang atau NOEL(S) berkurang dan elemen pada posisi TOP akan berubah. Operator POP ini tidak dapat digunakan pada stack kosong, artinya :

                        POP(CREATE(S)) = error condition

Catatan :  TOP(PUSH(E,S)) = E

created by Nurul Humaidi Abdillah TI-DG STIMIK ASIA

C. Deklarasi Stack Pada Bahasa Pemrograman

      Dalam bahasa pemrograman, untuk menempatkan stack biasanya digunakan sebuah array. Tetapi perlu diingat di sini bahwa stack dan array adalah dua hal yang berbeda. Misalkan suatu variabel S adalah sebuah stack dengan 100 elemen. Diasumsikan elemen S adalah integer dan jumlah elemennya maksimum adalah 100 elemen. Untuk mendeklarasikan stack dengan menggunakan array, harus dideklarasikan pula variabel lain yaitu TOP_PTR yang merupakan indeks dari array. Variabel TOP_PTR ini digunakan untuk menyatakan elemen yang berada pada posisi TOP dalam stack tersebut. Selanjutnya gabungan kedua variabel ini diberi nama STACK_STRUCT. Kemudian didefinisikan bahwa :

                  NOEL(S) = TOP_PTR

                  ISEMPTY(S) = TRUE, jika TOP_PTR = 0 dan

                                             FALSE, jika TOP_PTR > 0.

Maka bentuk deklarasinya dalam PASCAL adalah :

                  TYPE Stack_Struct = Record

                                                           Stack   : array[1..100] of integer;

                                                           TopPtr : integer;

                                                       End;

                  VAR S : Stack_Struct;

Selanjutnya, untuk keperluan operasi PUSH dan POP harus dibuat suatu prosedur tersendiri, yaitu :

                  PROCEDURE PUSH(Eon : integer);

                  Begin

                        If (S.TopPtr < NoelMax) Then Begin

                                                                        S.TopPtr := S.TopPtr + 1;

                                                                        S.Stack [S.TopPtr] := Eon

                                                                    End

                                                            Else Overflow_Condition

                  End;

                  PROCEDURE POP(Eoff : integer);

                  Begin

                        If (S.TopPtr > 0) Then Begin

                                                            Eoff := S.Stack[S.TopPtr];

                                                            S.TopPtr := S.TopPtr - 1

                                                         End

                                                Else Underflow_Condition 

                  End;

Overflow adalah suatu keadaan di mana kita melakukan operasi PUSH terhadap stack dalam keadaan penuh. Underflow adalah keadaan di mana kita melakukan operasi POP terhadap stack kosong. Eon adalah elemen yang akan dimasukkan ke dalam stack dan Eoff adalah elemen yang akan dikeluarkan dari dalam stack.

created by Nurul Humaidi Abdillah TI-DG STIMIK ASIA

NOTASI POSTFIX

          Bentuk aplikasi stack yang lain adalah mengubah suatu ekspresi aritmatik (string) ke dalam notasi postfix. Notasi postfix ini digunakan oleh compiler untuk menyatakan suatu ekspresi aritmatik dalam bahasa tingkat tinggi (high level language). Stack digunakan oleh compiler untuk mentransformasikan ekspresi aritmatik menjadi suatu ekspresi dalam bentuk/notasi postfix.

Contoh :

Misal diberikan ekspresi aritmatik : A + B ;

Maka bentuknya dalam notasi postfix menjadi : AB+

Urutan (prioritas) dari operator adalah :

      1.   Perpangkatan (^)

      2.   Perkalian (*) atau Pembagian (/)

      3.   Penjumlahan (+) atau Pengurangan (-)

Aturan yang digunakan dalam proses transformasi tersebut adalah :

1.      Ekspresi aritmatik yang diberikan di- "Scan" dari kiri ke kanan.

2.      Bila simbol yang di-scan adalah "(", maka simbol tersebut di push ke dalam stack. 

Bila simbol yang di-scan adalah ")", maka seluruh isi stack di pop keluar mulai dari simbol "(" yang pertama ditemukan dalam stack.

Bila simbol adalah operator, maka dilakukan perbandingan dulu dengan simbol (operator) yang berada pada posisi top dalam stack.

·        Jika derajatnya setara atau lebih rendah dari simbol yang berada pada posisi top, maka top stack di-pop keluar sebagai output dan simbol yang baru di-push ke dalam stack.

·        Jika derajatnya lebih tinggi dari simbol yang berada pada posisi top, maka simbol (operator) yang di-scan tersebut di-push ke dalam stack.

Bila simbol yang di-scan adalah operand, maka simbol tersebut langsung sebagai output.

Bila simbol adalah ";" maka seluruh isi stack di-pop sebagai output.

Proses Rekursif

         Stack juga dapat digunakan untuk menelurusuri suatu program atau procedure yang rekursif. Berikut ini sebuh contoh yang menyelesaikannya menggunakan proses rekursif.

Persoalan :

     Agar diperoleh uang sebanyak 1.000.000 rupiah pada 25 tahun yang akan datang,  berapakah banyak uang yang harus didepositokan saat ini? dianggap bahwa tingkat bunga tidak berubah selama 25 tahun yaitu sebesar 8% per/tahun.

      Penyelesaian :

      Untuk menyelesaikan masalah ini akan digunakan logika stack yaitu :

      - pada tahun ke-25 jumlah uang = Rp. 1.000.000,-

      - pada tahun ke-24 jumlah uang = Rp. 1.000.000 / (1 + 0.8)

      - pada tahun ke-23 jumlah uang =

                  .

               dst

     Berikut ini sebuah program PASCAL yang mengandung suatu procedure rekursif untuk menghitung jumlah uang diinginkan.

      PROGRAM DEPOSITO ;

      CONST          Goal = 1000000;

                              Rate = 0.08;

      VAR               Ju : Real;

                              Thn: Integer;

      PROCEDURE Hitung (VAR Thn : Integer);

      BEGIN

            IF (Thn > 0) THEN

                                                      BEGIN

                                                                  Ju := Ju/(1.0 + Rate);

                                                                  Thn := Thn - 1;

                                                                  Hitung(Thn);

                                                      END;

            END;

      BEGIN

            Thn := 25;

            Ju := Goal;

            HITUNG(Thn);

            WRITE(Ju);

      END.